Prof. Dr.-Ing. Johannes Schildgen
johannes.schildgen@oth-regensburg.de
Datenbanken
Kapitel 3: Das Relationenmodell
2020-10-30


In diesem Kapitel...
- ... lernen wir, dass eine Relation eine Tabelle ist,
- ... überführen wir ER-Diagr. in ein Relationenschema,
- ... wenden wir relationale Algebra an,
- ... schauen wir uns drei Normalformen an.
Relation (= Tabelle)
Metadaten
- Name der Relation (= Tabellennname)
- Attribute (= Spalten)
- Datentypen und Eigenschaften der Attribute
(Primärschlüssel, Fremdschlüssel, ...)
Daten
- Menge von Tupeln (= Zeilen)
- Tupel besitzt einen Wert in jedem Attribut
Relation: Produkte
Metadaten
PRODUKTE(produktnummer,bezeichnung,preis,hersteller)
W(produktnummer) = integer,
W(bezeichnung) = string, usw.
Daten
PRODUKTE = {(17, Schokoriegel, 0.89, Monsterfood), ...}
Relation = Menge von Tupeln
R(A1,A2,...) ⊆ W(A1) ⨯ W(A2) ⨯ ...
- Mengen haben keine Duplikate
- Mengen haben keine Ordnung
- Ordnung der Attribute spielt keine Rolle
NULL-Werte
NULL = nicht vorhandener Wert
Mögliche Bedeutungen für Preis IS NULL:
- Der Preis ist unbekannt
- Das Produkt ist ausverkauft
- Produkte dieser Art haben keinen Preis
- Preis nur auf Anfrage
Was könnte PREIS IS NULL bedeuten?
- Der Preis ist unbekannt
- Das Produkt ist ausverkauft
- Produkte dieser Art haben keinen Preis
- Preis nur auf Anfrage
https://frage.space
Primärschlüssel
PK ⊆ {A1, A2, ...}
- Primärschlüssel identifiziert Tupel eindeutig
- Es darf Relationen ohne Primärschlüssel geben
- Primärschlüssel ist eindeutig:
Es darf keine zwei verschiedene Tupel in der Relation geben, die in den Primärschlüsselattributen die gleichen Werte haben. - Primärschlüssel dürfen keine NULL-Werte enthalten
Beispiel: hersteller
- Der Firmenname eines Herstellers ist eindeutig
- Der Firmenname darf nicht NULL sein
- Das Land darf NULL sein
Fremdschlüssel
- Mit Fremdschlüsseln werden Beziehungen
Wert-basiert modelliert - Fremdschlüssel referenziert Attributmenge
- Fremdschlüsselattribute haben die gleichen Datentypen wie die referenzierten Attribute
- In Fremdschlüsselattributen dürfen nur Werte stehen, die auch tatsächlich in der referenzierten Relation in den referenzierten Attributen existieren; NULL ist aber auch erlaubt
Beispiel: produkte und hersteller
produkte.hersteller ist Fremdschlüssel auf hersteller.firma
Zusammengesetzte Schlüssel
produkte(hersteller,land) ist Fremdschlüssel auf hersteller(firma,land)
Zusammengesetzte Schlüssel
termine
| Datum | Uhrzeit | Raum | Dauer | Bezeichnung |
|---|---|---|---|---|
| 2020-10-14 | 14:15 | 17-123 | 90 | Dings-Meeting |
| 2020-10-21 | 16:00 | 17-222 | 60 | Treffen mit Jürgen |
personen
nehmen_teil
| PersNr | Datum | Uhrzeit | Raum |
|---|---|---|---|
| 5 | 2020-10-14 | 14:15 | 17-123 |
| 8 | 2020-10-14 | 14:15 | 17-123 |
| 5 | 2020-10-21 | 16:00 | 17-222 |
nehmen_teil.persnr ist Fremdschlüssel auf personen.persnr
nehmen_teil(datum,uhrzeit,raum) ist Fremdschl. auf termine(datum,uhrzeit,raum)
Transformation
ER-Diagramm → Relationenmodell
| ER-Diagramm | Relationenmodell | |
|---|---|---|
| Entitätstyp | → | Relation (=Tabelle) |
| Attribut | → | Attribut (=Spalte) |
| Primärschlüssel | → | Primärschlüssel |
| Sub-Attribute | → | Einzelne Attribute |
| Mehrwertiges Attribut | → | Relation |
| 1:N-Beziehung | → | Fremdschlüssel |
| N:M-Beziehung | → | Relation |
| Schwache Entitätstypen | → | Relation |
| Generalisierung | → | Relation(en) |
Entitätstyp → Relation
| Entitätstyp | → | Relation (=Tabelle) |
| Attribut | → | Attribut (=Spalte) |
| Primärschlüssel | → | Primärschlüssel |
Sub-Attribute → Einzelne Attribute
Personen(
PersNr,
Name,
Adresse_Strasse,
Adresse_PLZ,
Adresse_Ort
)
Wie viele Attribute hat die Tabelle Personen?
- 2
- 3
- 5
- 6
https://frage.space
Mehrwertiges Attribut → Relation
Personen
Telefonnummern
| PersNr | Telefon |
|---|---|
| 4 | 0151-1 |
| 4 | 0151-2 |
| 5 | 0151-3 |
telefonnummern.persnr ist Fremdschlüssel auf personen.persnr
1:N-Beziehung → Fremdschlüssel
produkte.hersteller ist Fremdschlüssel auf hersteller.firma
Rekursive Beziehung → Fremdschl.
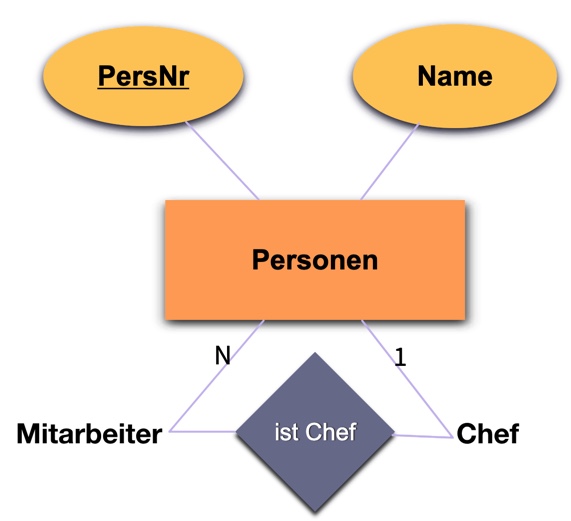
personen.chef ist Fremdschlüssel auf personen.persnr
Darf eine Person sein eigener Chef sein (also Chef=PersNr)?
- Ja sicher
- Nee, das geht nicht
https://frage.space
N:M-Beziehung → Relation
kunden_bewerten_produkte.kundennr
ist Fremdschlüssel auf kunden.kundennr
kunden_bewerten_produkte.produktnr
ist Fremdschlüssel auf produkte.produktnr
Schwache Entitätstypen → Relation
Anbieter(
Anbieternr,
Anbietername
)
Handytarife(
Anbieternr,
Tarifbezeichnung,
Datenvolumen,
Preis
)
handytarife.anbieternr ist
Fremdschlüssel auf anbieter.anbieternr
Schwache Entitätstypen → Relation
Kunden(Kundennr, ...)
Produkte(Produktnr, ...)
Bewertungen(Kundennr, Produktnummer, Sterne, Text)
bewertungen.kundennr ist Fremdschlüssel auf kunden.kundennr
bewertungen.produktnr ist Fremdschlüssel auf produkte.produktnr
Dieses Relationenschema ist das gleiche wie...
- wenn Bewertungen nicht schwach wäre
- bei der N:M-Beziehung "bewertet"
- bei einem mehrwertigen Attribut "Bewertung"
- bei einer ternären Beziehung "bewertet"
https://frage.space
Ternäre Beziehung → Relation
Buchung(Kundennr, Studio_Str, Studio_Hausnr, Tarif_Bezeichnung, Datum)
buchung.kundennr ist Fremdschlüssel auf kunden.kundennr
buchung.tarif_bezeichnung ist Fremdschlüssel auf tarife.bezeichnung
buchung(studio_str, studio_hausnr) ist FK auf fitnessstudios(strasse, hausnummer)
Wenn bei Tarife keine 1, sondern ein L stünde...
- hätte das keine Auswirkung auf das Relationenschema
- müsste man eine weitere Relation erstellen
- gehörte Tarif_Bezeichnung zum Primärschlüssel
- hä? Kommt nach N, M, nicht O?
https://frage.space
NOT NULL / UNIQUE
⇒ Geburtsort ist NOT NULL
⇒ Geburtsort ist UNIQUE
⇒ Geburtsort ist UNIQUE NOT NULL
NOT NULL / UNIQUE
Personen(
PersNr,
Name,
E-Mail,
Geburtsort NOT NULL,
Kreditkarte UNIQUE
)
Generalisierung im Relationenmodell
Mehrere Möglichkeiten
der Umsetzung:
- Volle Redundanz
- Hausklassenmodell
- Vertikale Partitionierung
- Hierarchierelation
Volle Redundanz
- Jeder Entitätstyp wird zur eigenständigen Relation (alle Spalten)
- Beim Einfügen in Sub-Relationen wird redundante Information in die entsprechenden Super-Relationen eingefügt.
Kunden(Kundennr, Name, E-Mail)
Privatkunden(Kundennr, Name, E-Mail, Bonuspunkte)
Geschäftskunden(Kundennr, Name, E-Mail, USt-ID)
Privatkunden.Kundennr und
Geschäftskunden.Kundennr sind Fremdschlüssel
auf Kunden.Kundennr.
Volle Redundanz
Hausklassenmodell
- Jeder Entitätstyp wird zur eigenständigen Relation (alle Spalten)
- Es wird nur in die speziellste Relation eingefügt.
Kunden(Kundennr, Name, E-Mail)
Privatkunden(Kundennr, Name, E-Mail, Bonuspunkte)
Geschäftskunden(Kundennr, Name, E-Mail, USt-ID)
Hier keine Fremdschlüssel.
Woran erkennt man im Relationenschema den Unterschied zwischen dem Hausklassenmodell und der vollen Redundanz?
- Es gibt keinen Unterschied
- Weniger Spalten beim Hausklassenmodell
- Mehr Spalten beim Hausklassenmodell
- Bei der vollen Redundanz gibt es Fremdschlüssel
https://frage.space
Hausklassenmodell
Vertikale Partitionierung
- Jeder Entitätstyp wird zur eigenständigen Relation
(PK + spezielle Spalten)
Kunden(Kundennr, Name, E-Mail)
Privatkunden(Kundennr, Bonuspunkte)
Geschäftskunden(Kundennr, USt-ID)
Privatkunden.Kundennr und
Geschäftskunden.Kundennr sind Fremdschlüssel
auf Kunden.Kundennr.
Vertikale Partitionierung
Hierarchierelation
- Nur eine einzige Relation mit ALLEN Spalten.
- Type_Tag gibt den Entitätstypen an
Kunden(Kundennr, Name, E-Mail, Bonuspunkte, USt-ID, Type_Tag)
Relationale Algebra
Die Relationale Algebra besteht aus Operationen, die auf ein oder mehreren Relationen angewendet werden können. Das Ergebnis einer solchen Operation ist wieder eine Relation.
Beispiel: Vereinigung
RelaX - relational algebra calculator
https://dbis-uibk.github.io/relax/
Gist-ID unseres Webshop-Schemas: d67f16874b528abc6e6c88d07a50b2dc
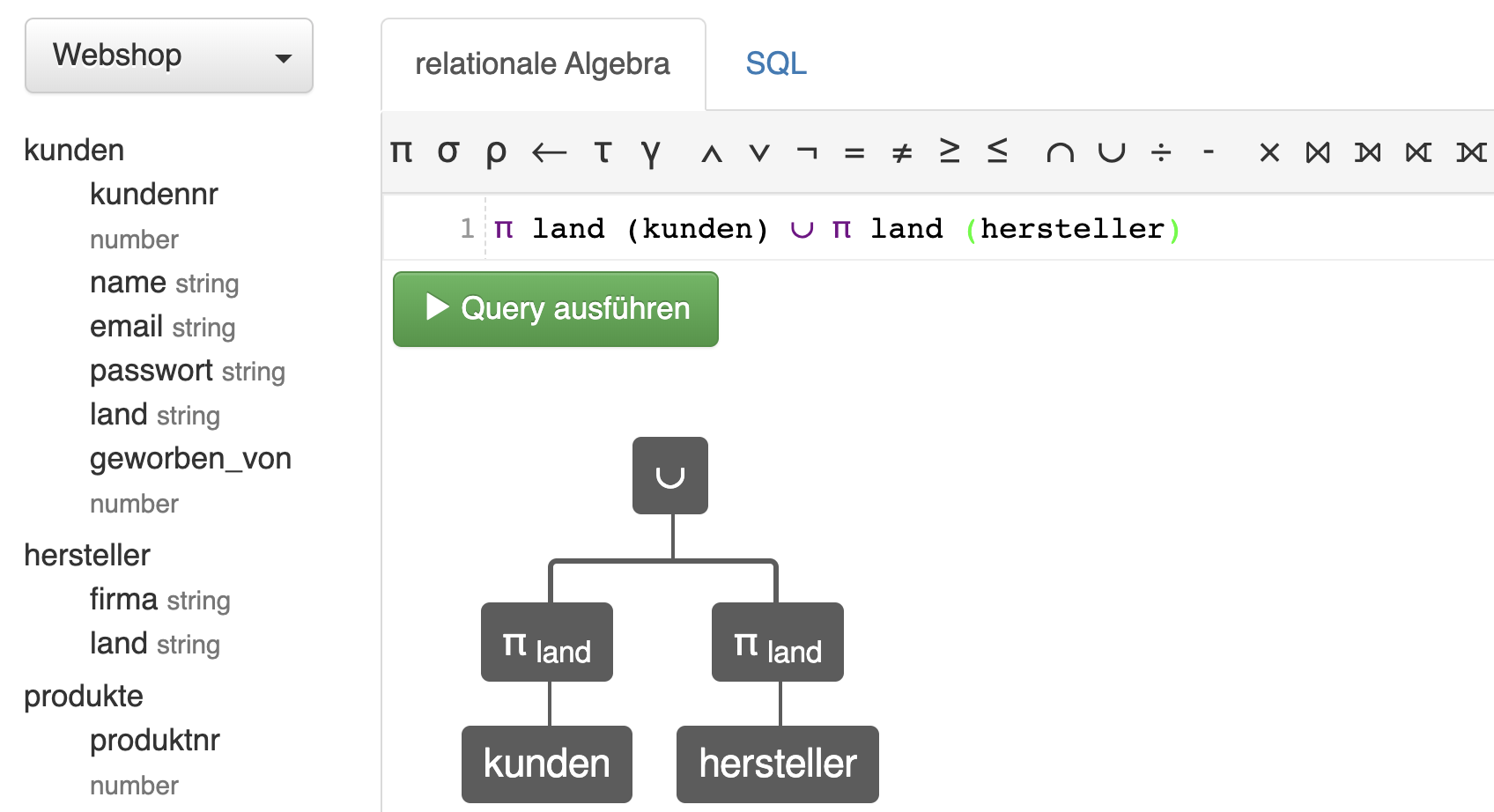
Mengenoperationen
- Relationen sind Mengen von Tupeln
- Mengen können vereinigt, geschnitten und voneinander subtrahiert werden
- Das geht aber nur, wenn die Mengen vereinigungsverträglich sind
Vereinigungsverträglichkeit
- Gleiche Anzahl von Spalten
- Kompatible Datentypen
⋂ Schnittmenge
Diejenigen Zeilen, die in beiden Relationen vorkommen.
\ Mengensubtraktion
Die Zeilen der ersten ohne die der zweiten Relation.
⋃ Vereinigung
Alle Zeilen aus beiden Relationen.
π Projektion
$\pi_{A_1, A_2, \dots, A_n}(R)$
Beschränkung der Relation $R$ auf die Spalten $A_1, A_2, \dots, A_n$
$\pi_{kundennr, name}(Kunden)$
Wie viele Zeilen kommen bei einer Projektion auf einer nicht leeren Relation R heraus?
- Genau |R|
- Zwischen 0 und |R|
- Zwischen 1 und |R|
- Zwischen |R| und ∞
https://frage.space
π Projektion
Achtung: Duplikateliminierung!
$\pi_{hersteller}(Produkte)$
σ Selektion
$\sigma_{P}(R)$
Auswahl derjenigen Zeilen der Relation $R$, die das Kriterium $P$ erfüllen.
$\sigma_{hersteller='Monsterfood'}(Produkte)$
Selektion
$\sigma_{preis>1}(\sigma_{hersteller='Monsterfood'}(Produkte))$
Klammern weglassen:
$\sigma_{preis>1}\sigma_{hersteller='Monsterfood'}(Produkte)$
Selektionen mit AND verbinden:
$\sigma_{preis>1 \wedge hersteller='Monsterfood'}(Produkte)$
OR geht so:
$\sigma_{preis>1 \vee hersteller='Monsterfood'}(Produkte)$
Das entspricht:
$\sigma_{preis>1}(Produkte) \cup \sigma_{hersteller='Monsterfood'}(Produkte)$
Operatorabfolgen
"Von welchen Herstellern aus Österreich gibt es keine Produkte?"
- Welche Hersteller sind aus Österreich?
$\sigma_{land='Österreich'}(Hersteller)$ - Wie heißen diese Hersteller?
$\pi_{firma}\sigma_{land='Österreich'}(Hersteller)$ - Vor welchen Herstellern sind unsere Produkte?
$\pi_{hersteller}(Produkte)$ - Subtraktion von 2. und 3.:
$\pi_{firma}\sigma_{land='Österreich'}(Hersteller) \setminus \pi_{hersteller}(Produkte)$
Operatorbäume
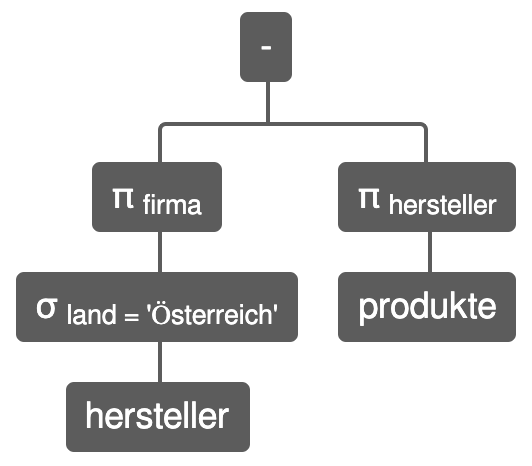
⨯ Kartesisches Produkt
"Jedes mit jedem"
$Produkte \times Bewertungen$
Tabellenprefix
Der Name der Relation kann bei Attributen als Prefix angegeben werden.
$\sigma_{Produkte.Produktnr=Bewertungen.Produktnr}(Produkte \times Bewertungen)$
ρ Umbenennungsoperator
Relation umbenennen
$\rho_{P1}(Produkte)$
Attribut umbenennen
$\rho_{bez\leftarrow bezeichnung}(Produkte)$
Welche Produkte kosten mehr als die Spülmaschinentabs?
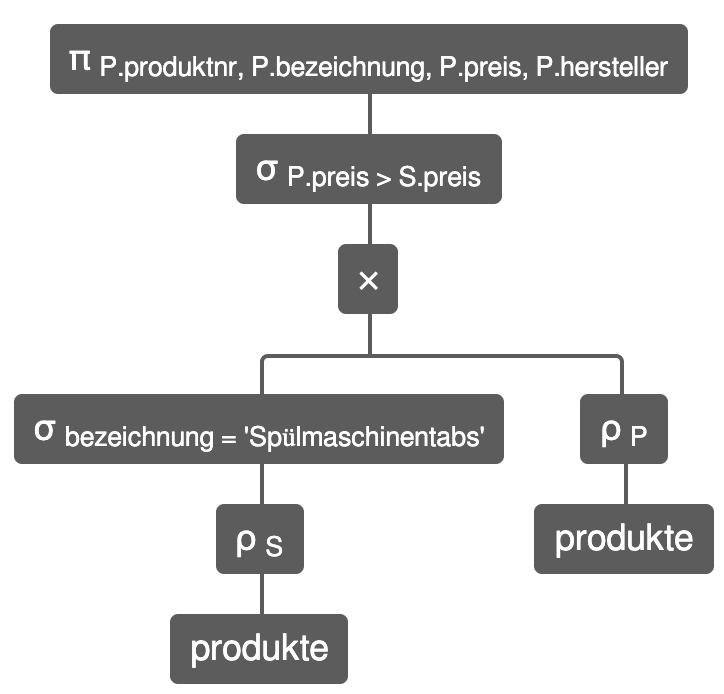
⋈ Join (Verbund)
Ein Join ist ein Kreuzprodukt mit anschließender Selektion, welche die Spaltenwerte der beiden Relationen vergleicht
Gleichverbund (Equi-Join)
$R \bowtie_{P}S = \sigma_{P}(R \times S)$
Welche Produkte sind von einem Hersteller aus den USA?
$\pi_{Bezeichnung}\sigma_{Land='USA'}(Produkte \bowtie_{Produkte.Hersteller=Hersteller.Firma}Hersteller)$
Es gilt: $R ⋈ S = S ⋈ R$
Suche nach Join-Partnern
$Produkte \bowtie_{Produkte.Hersteller=Hersteller.Firma}Hersteller$
Ergebnis des Joins
$Produkte \bowtie_{Produkte.Hersteller=Hersteller.Firma}Hersteller$
Der Join ist verlustbehaftet.
Was ist verloren gegangen?
- Produkte mit Hersteller NULL
- Hersteller, von denen es keine Produkte gibt
- beides
- gar nichts
https://frage.space
Verlustfreier Join
$Produkte \bowtie_{Produkte.Hersteller=Hersteller.Firma}Hersteller$
Rekonstruktion der Tabellen
$produkte = \pi_{produktnr, bezeichnung, preis, hersteller}(V)$
$hersteller = \pi_{firma, land}(V)$
Äußerer Verbund
$\bowtie$ Innerer Verbund
Nur die Zeilen, die Join-Partner finden, sind im Ergebnis
$⟕$ Linker äußerer Verbund
Alle Zeilen der linken Relation sind definitiv im Ergebnis
$⟖$ Rechter äußerer Verbund
Alle Zeilen der rechten Relation sind definitiv im Ergebnis
$⟗$ Voller äußerer Verbund
Alle Zeilen beider Relation sind definitiv im Ergebnis
$⟕$ Linker äußerer Verbund
$Produkte ⟕_{Produkte.Hersteller=Hersteller.Firma}Hersteller$
$⟖$ Rechter äußerer Verbund
$Produkte ⟖_{Produkte.Hersteller=Hersteller.Firma}Hersteller$
Es gilt: $R ⟖ S = S ⟕ R$
$⟗$ Voller äußerer Verbund
$Produkte ⟗_{Produkte.Hersteller=Hersteller.Firma}Hersteller$
Es gilt: $R ⟗ S = S ⟗ R$
Join-Varianten
Innerer / linker / rechter / voller äußerer Join
$R \bowtie_{P} S$ $R ⟕_{P} S$ $R ⟖_{P} S$ $R ⟗_{P} S$
Gleichverbund (Equi-Join)
$R \bowtie_{R.a = S.x \wedge R.b = S.y \wedge \dots} S$
Theta-Join
$R \bowtie_{R.a \theta S.x \wedge \dots} S$ mit $\theta \in \{<,≤,=,≠,≥,>\}$
Beispiele: Equi-/Theta-Joins
Finde zu jedem Produkt seinen Hersteller:
$produkte \bowtie_{Produkte.Hersteller=Hersteller.Firma}hersteller$
Finde zu jedem Produkt teurere Produkte als es selbst:
$\rho_{P1}(produkte) \bowtie_{P1.preis < P2.preis} \rho_{P2}(produkte)$
Join-Varianten
Natürlicher Verbund (natural Join)
$R \bowtie S$
Gleichverbund über die gleich heißenden Attribute. Im Ergebnis sind solche Attribute nur einmal vorhanden.
Self-Join
$R \bowtie_P R$
Semi-Join
$R \ltimes_P S = \pi_{R.*}(R \bowtie_P S)$
Welcher Join-Bedingung entspricht ein natürlicher Verbund zwischen A(x,y,z) und B(s,t,x,y)?
- A.x = B.s
- A.x = B.x
- A.y = B.y
- A.x = B.x ∧ A.y = B.y
https://frage.space
Beispiel: Natürlicher Verbund
$produkte \bowtie bewertungen$
Entspricht:
$\pi_{produkte.produktnummer, bezeichnung, preis, hersteller, kundennr, sterne, bewertungstext}$
$(produkte \bowtie_{produkte.produktnr = bewertungen.produktnr} bewertungen)$
Beispiel: Self-Join
$\rho_{K1}(personen) \bowtie_{K1.chef = K2.persnr} \rho_{K2}(personen)$
Beispiel: Semi-Join
$produkte \ltimes_{produkte.produktnr=bewertungen.produktnr} bewertungen $
Alle Produkte, die schon einmal bewertet wurden.
÷ Division
$R \div S$
Diejenigen Tupel aus R (ohne die Spalten von S), die in jeder Kombination mit allen Tupeln aus S vorkommen.
Es gilt: $(R \times S) \div S = R$
Beispiel: Division
Welche Kunden haben alle Produkte bewertet?
$\pi_{kundennr, produktnr}(bewertungen)$
$\pi_{produktnr}(produkte)$
$\pi_{kundennr, produktnr}(bewertungen) \div \pi_{kundennr}(kunden)$
Anfrageoptimierung
"Wie heißen die Produkte, die Kunde Nr. 5 bewertet hat?"
Äquivalente Ausdrücke:
- $\pi_{bezeichnung}\sigma_{kundennr=5}\sigma_{produkte.produktnr=bewertungen.produktnr}(produkte\times bewertungen)$
- $\pi_{bezeichnung}(\pi_{produktnr, bezeichnung} produkte\bowtie \pi_{produktnr}\sigma_{kundennr=5}(bewertungen))$
- $\pi_{bezeichnung}\sigma_{kundennr=5}(produkte\bowtie bewertungen)$
- $\pi_{bezeichnung}(produkte\bowtie \sigma_{kundennr=5}(bewertungen))$
Welcher Ausführungsplan ist besser / "billiger"?
Welcher Plan ist der beste?
- a.
- b.
- c.
- d.
https://frage.space
Anfrageoptimierung
Überführung eines Ausdrucks in einen äquivalenten möglichst effizient auszuführenden Ausdruck.
Kostenbasierte Optimierer
Jeder Ausführungsplan erhält Kostenschätzung.
Der Plan mit den geringsten Kosten wird gewählt.
Beispiel: Kosten = Größe der Zwischenergebnisse
100.000 Kunden, 500.000 Bewertungen. Schätzen Sie:
|σ kundennr=5 (bewertungen)|
- 0
- 1
- 5
- 100.000
https://frage.space
Beispiel: Anfrageoptimierung
Annahme: 100.000 Kunden, 500.000 Bewertungen, 300.000 Produkte
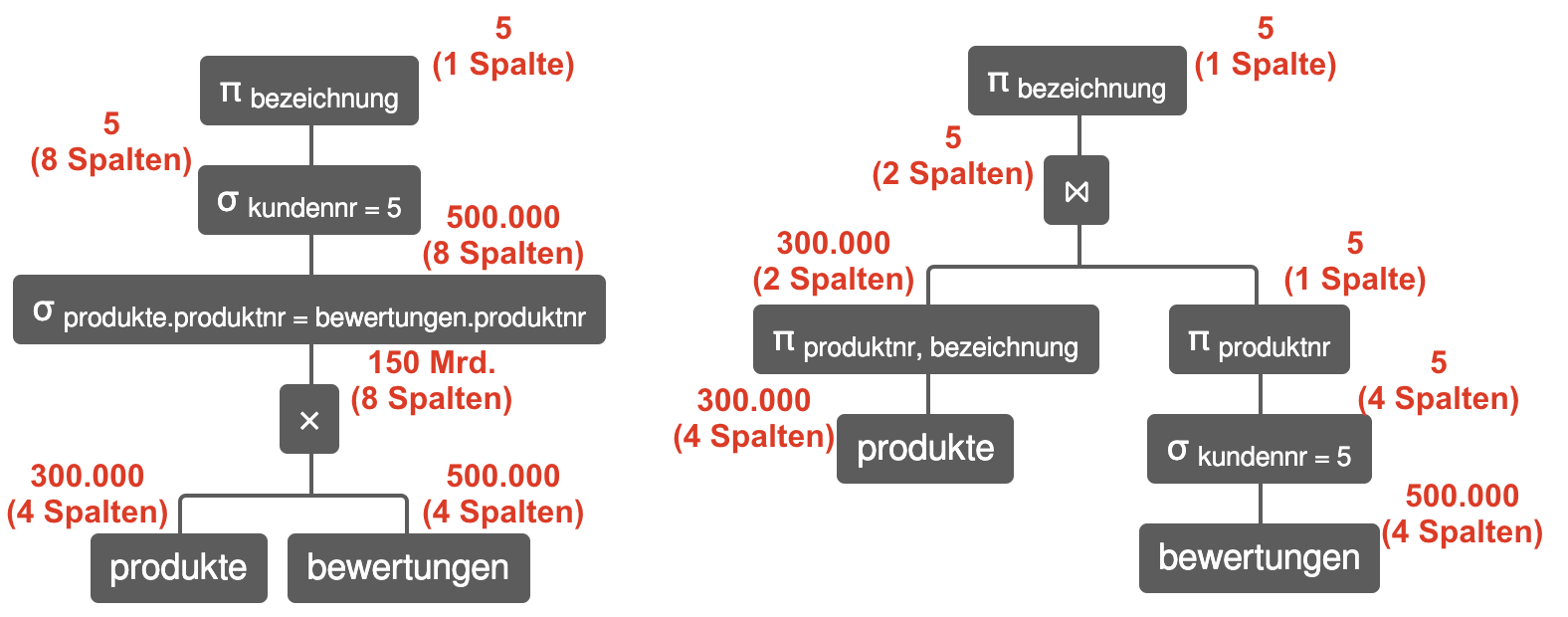
Heuristiken
- Frühstmögliche Selektion
- Join statt Kreuzprodukt
- Frühstmögliche Projektion (ohne Duplikateliminierung)
- Join-Reihenfolge so wählen, dass Zwischenergebnisse klein sind
- Folgen von Selektionen und Projektionen zusammenfassen
- Selektionen statt Mengenoperationen
- Nichts doppelt berechnen
Heuristiken
Frühstmögliche Selektion
Vorher: $\sigma_{kundennr=5}(produkte \bowtie bewertungen)$
Nachher: $produkte \bowtie \sigma_{kundennr=5}(bewertungen)$
Join statt Kreuzprodukt
Vorher: $\sigma_{produkte.produktnr=bewertungen.produktnr}(produkte \times bewertungen)$
Nachher: $produkte \bowtie_{produkte.produktnr=bewertungen.produktnr} (bewertungen)$
Frühstmögliche Projektion (ohne Duplikateliminierung)
Vorher: $\pi_{bezeichnung}(produkte \bowtie bewertungen)$
Nachher: $\pi_{bezeichnung}(\pi_{produktnr, bezeichnung}(produkte) \bowtie bewertungen)$
Warum haben wir nach der Optimierung zwei Projektionsoperationen in der Anfrage?
- Wegen der Sicherheit
- Wegen der Redundanz
- Wegen der Einfachheit
- Wegen des Joins
https://frage.space
Heuristiken
Join-Reihenfolge so wählen,
dass Zwischenergebnisse klein sind
Vorher: $(kunden \bowtie bewertungen) \bowtie \sigma_{hersteller='Monsterfood'}(produkte)$
Nachher: $(bewertungen \bowtie \sigma_{hersteller='Monsterfood'}(produkte)) \bowtie kunden$
Folgen von Sel. und Proj. zusammenfassen
Vorher: $\pi_{bezeichnung}\pi_{produktnr,bezeichnung}\sigma_{preis \le 5}\sigma_{hersteller='Monsterfood'}produkte$
Nachher: $\pi_{bezeichnung}\sigma_{preis \le 5 \wedge hersteller='Monsterfood'}produkte$
Selektionen statt Mengenoperationen
Vorher: $\sigma_{hersteller='Monsterfood'}(produkte) \cup \sigma_{hersteller='Calgonte'}(produkte)$
Nachher: $\sigma_{hersteller='Monsterfood' \vee hersteller='Calgonte'}(produkte)$
Kardinalitätsschätzung
Wie viele Tupel sind im Ergebnis einer Operation zu erwarten?
Hilfreiche Statistiken:
- Kardinalitäten der Tabellen (Anzahl Zeilen)
- Kardinalitäten der Spalten (Anzahl distinkter Werte)
- Kleinster, größter Wert je Spalte, Median, ...
- Werte-Histogramme (Häufigkeitsverteilung)
- Erfahrungen über Verschätzungen in der Vergangenheit (→ lernende Optimierer)
- ...
Kardinalitätsschätzung: Selektion
Annahme: Gleichverteilung
|R| (Anzahl Zeilen in R)
|R.a| (Anzahl distinkter Werte in Spalte R.a)
$|\sigma_{R.a = x}(R)| = \frac{|R|}{|R.a|}$
Beispiel:
$|\sigma_{geschlecht='weiblich'}(Personen)| = \frac{1}{3} |Personen|$
Kardinalitätsschätzung: Selektion
Selektivitätsfaktor $sf_P$: $|\sigma_P R|=sf_P \cdot |R|$
Annahme: Werteunabhängigkeit
$sf_{P \wedge Q} = sf_P \cdot sf_Q$
Beispiel:
3 verschiedene Geschlechter, 1000 verschiedene Vornamen
$|\sigma_{geschlecht='weiblich' \wedge vorname='Peter'}(Personen)|$ $ = \frac{1}{3} \cdot \frac{1}{1000} |Personen|$
Was kommt raus?
- 1/3 Personen
- 1/1000 Personen
- 1/1003 Personen
- 1/3000 Personen
https://frage.space
$|\sigma_{geschlecht='männlich' \wedge vorname='Peter'}(Personen)| = \frac{1}{3} \cdot \frac{1}{1000} |Personen|$
Kardinalitätsschätzung: ⨯
$|R \times S| = |R| \cdot |S|$
Beispiel: $|kunden \times kunden| = |kunden|^2$
Kardinalitätsschätzung: ⋈
$|R \bowtie_{R.a=S.a} S|$
Im Allgemeinen:
$0 \le |R \bowtie_{R.a=S.a} S| \le |R| \cdot |S|$
Wenn R.a Fremdschlüssel auf S.a ist:
$|R \bowtie_{R.a=S.a} S = |R|$
Beispiel: |$produkte \bowtie bewertungen| = |bewertungen|$
Normalformenlehre
- Was ist ein gutes DB-Schema?
- Funktionale Abhängigkeiten
- Superschlüssel, Schlüsselkandidaten
- Normalformen: 1NF, 2NF, 3NF
Ist dies ein gutes DB-Schema?
| cd_id | tracknr | album | band | land | song |
|---|---|---|---|---|---|
| 101 | 1 | Jupiter | Eddy G. | DE | All ducks |
| 101 | 2 | Jupiter | Eddy G. | DE | Far away |
| 202 | 1 | Mars | Eddy G. | DE | Meersalz |
| 202 | 2 | Mars | Eddy G. | DE | Mehr Salz |
| 303 | 1 | Stone | Bob 88 | EN | I'm 88 |
Was ist an diesem Schema nicht so gut?
- Inkonsistenz
- Redundanz
- Unverständlich
- Falscher Primärschlüssel
https://frage.space
Anomalien bei Redundanzen
| cd_id | tracknr | album | band | land | song |
|---|
Einfügeanomalie
Wir können keine neue Band hinzufügen, wenn sie noch kein Album herausgebracht hat.
Änderungsanomalie
Wenn wir das Land einer Band ändern, muss diese Änderung an vielen Stellen erfolgen.
Löschanomalie
Wenn wir das letzte Album einer Band löschen, verlieren wir die Band-Infos.
Funktionale Abhängigkeit
$A$ und $B$ sind Attributmengen aus der Relation $R$
$A \rightarrow B$ (lies: A bestimmt B)
Immer wenn zwei Zeilen in $R$ die gleichen Werte in den
$A$-Attributen haben, dann sind auch die Werte in den
$B$-Attributen gleich.
Beispiel: $band \rightarrow land$
Funktionale Abhängigkeiten
Es gilt: $cd\_id \rightarrow album; cd\_id \rightarrow band; band \rightarrow land;$
$cd\_id, tracknr \rightarrow song$
Welche funktionalen Abhängigkeiten gilt hier NICHT?
- cd_id, tracknr → cd_id
- cd_id, tracknr → album, tracknr
- cd_id → land
- song → tracknr
https://frage.space
Volle funktionale Abhängigkeit
$A \Rightarrow B$ (lies: A bestimmt B voll-funktional)
Dies ist der Fall wenn
- $A \rightarrow B$ und
- $\not \exists X \subset A: X \rightarrow B$
Beispiel: $cd\_id, tracknr \rightarrow land$
Aber nicht: $cd\_id, tracknr \Rightarrow land$, weil bereits $cd\_id \rightarrow land$
Superschlüssel
Die Attributmenge $A$ ist Superschlüssel der Relation R, genau dann wenn $A \rightarrow R$ (sie bestimmt alle Attribute)
Ist cd_id Superschlüssel?
$cd\_id \rightarrow album; cd\_id \rightarrow band; band \rightarrow land;$
$\Rightarrow cd\_id \rightarrow cd\_id, album, band, land$
$\Rightarrow cd\_id$ ist kein Superschlüssel (z. B. $cd\_id \not\rightarrow tracknr$)
Ist cd_id, tracknr Superschlüssel?
$cd\_id \rightarrow album; cd\_id \rightarrow band; band \rightarrow land; cd\_id, tracknr \rightarrow song$
$\Rightarrow cd\_id, tracknr \rightarrow cd\_id, tracknr, album, band, land, song = R$
$\Rightarrow cd\_id, tracknr$ ist Superschlüssel
Schlüsselkandidat
Die Attributmenge $A$ ist Schlüsselkandidat von R, wenn
- $A$ Superschlüssel ist und
- keine echte Teilmenge von $A$ Superschlüssel ist.
Ein Schlüsselkandidat ist ein minimaler Superschlüssel.
Ist cd_id, tracknr Schlüsselkandidat?
- cd_id, tracknr ist Superschlüssel (siehe vorherige Folie)
- cd_id ist kein Superschlüssel (siehe vorherige Folie)
- tracknr ist kein Superschlüssel (nur $tracknr \rightarrow tracknr$)
$\Rightarrow cd\_id, tracknr$ ist Schlüsselkandidat
{cd_id, tracknr, song} ist ein...
- Superschlüssel
- Schlüsselkandidat
- beides
- weder noch
https://frage.space
1. Normalform (1NF)
Eine Relation ist in erster Normalform, wenn alle ihre Attribute weder zusammengesetzt noch mengenwertig noch relationenwertig sind.
=> Ist hier der Fall! Die Relation ist in 1NF.
(NF)2 = Non First Normal Form
| pizza_id | bezeichnung | zutaten | preis | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | Spezial | Salami, Schinken, Pilze |
| ||||||
| 2 | Hawaii | Ananas, Schinken |
|
Zutaten ist ein mengenwertiges Attribut, Preis ist ein relationenwertiges Attribut.
=> Nicht in 1NF.
Überführung in 1NF
Attribute flachklopfen.
| pizza_id | bezeichnung | zutat |
|---|---|---|
| 1 | Spezial | Salami |
| 1 | Spezial | Schinken |
| 1 | Spezial | Pilze |
| ... | ... | ... |
| pizza_id | bezeichnung | größe | preis |
|---|---|---|---|
| 1 | Spezial | klein | 7.00 |
| 1 | Spezial | groß | 8.50 |
| ... | ... | ... | ... |
Jetzt ist das Schema in 1NF.
Welche volle funktionale Abhängigkeit gilt in der obigen Tabelle?
- pizza_id ⇒ bezeichnung
- pizza_id, zutat ⇒ bezeichnung
- zutat ⇒ bezeichnung
- pizza_id, bezeichnung ⇒ zutat
https://frage.space
2. Normalform (2NF)
Eine Relation ist in zweiter Normalform, wenn sie in 1NF ist und jedes Nicht-Schlüsselattribut voll vom ganzen Schlüssel abhängt.
Ist Pizza1(pizza_id, bezeichnung, zutat) in 2NF?
Überprüfe für Nicht-Schlüsselattribut "bezeichnung": $pizza\_id, zutat \Rightarrow bezeichnung$ ?
Nicht der Fall, weil bereits $pizza\_id \rightarrow bezeichnung$
Damit ist die Relation nicht in 2NF.
Überführung in 2NF
Zerlegung in Relationen, die den Teil der Schlüsselattribute besitzen, von dem die jeweiligen Nicht-Schlüssel-Attribute voll funktional abhängen.
Gegeben: Pizza1(pizza_id, bezeichnung, zutat)
$pizza\_id \rightarrow bezeichnung$
Resultat in 2NF: Pizza1a(pizza_id, zutat) und Pizza1b(pizza_id, bezeichnung)
Wichtig bei Zerlegungen: Zerlegung muss verlustfrei erfolgen und ein Join der neuen Tabellen muss wieder die ursprüngliche Tabelle ergeben.
CD-Track-Beispieltabelle
| cd_id | tracknr | album | band | land | song |
|---|
$cd\_id \rightarrow album; cd\_id \rightarrow band; band \rightarrow land; cd\_id, tracknr \rightarrow song$
Ist die Tabelle in 2NF?
Ist die Tabelle in 2NF?
- Ja, weil z. B. {cd_id, tracknr} ⇒ album
- Nein, weil cd_id → tracknr
- Nein, weil cd_id → album
- Nein, weil tracknr → album
https://frage.space
Überprüfe für Nicht-Schlüsselattribut "album", ob $cd\_id, tracknr \Rightarrow album$ ?
Nein, weil $cd\_id \rightarrow album$ ⇒ Die Relation ist also nicht in 2NF
Überführung in 2NF:
- Tracks(cd_id,tracknr, song)
- Alben(cd_id, album, band, land)
3. Normalform (3NF)
Eine Relation ist in dritter Normalform, wenn sie in 2NF ist und es keine nicht-trivialen transitiven Abhängigkeiten zwischen Nicht-Schlüsselattributen gibt.
Triviale Abhängigkeit: $A \rightarrow X$ mit $X \subseteq A$
Transitive Abhängigkeit: $A \rightarrow B; B \rightarrow C$
Ist Alben(cd_id, album, band, land) in 3NF?
Ist Alben(cd_id, album, band, land) in 3NF?
- Ja, weil es keine transitiven Abhängigkeiten gibt
- Nein, weil cd_id → band; band → land
- Nein, weil cd_id, band → cd_id; cd_id → band
- Ich weiß es nicht! Ich weiß es einfach nicht!!!
https://frage.space
Nein, weil es folgende transitive Abhängigkeit gibt:
$cd\_id \rightarrow band; band \rightarrow land$
Überführung in 3NF
Transitive Abhängigkeit: $A \rightarrow B; B \rightarrow C$
Entfernen von C aus der Relation
Neue Relation hat Attribute B (Primärschlüssel) und C
Gegeben: Alben(cd_id, album, band, land)
$cd\_id \rightarrow band; band \rightarrow land$
Resultat in 3NF:
- Alben(cd_id, album, band)
- Bands(band, land)
Kapitelzusammenfassung
- Relation/Tabelle = Menge von Tupeln
- Primärschlüssel, Fremdschlüssel, NULL-Werte
- Überführung ER → Relationenschema
- Relationale Algebra: $\pi, \sigma, \bowtie, \times, \cup, \div, \dots$
- Join: Inner, Left/Right/Full Outer, ...
- Anfrageoptimierung / Heuristiken
- Funktionale Abhängigkeiten
- Superschlüssel, Schlüsselkandidaten
- Normalformen: 1NF, 2NF, 3NF